Kaprekar's Constant

Intro
this article was pulled from a twitter thread that I wrote here
Math is really magical. It's filled with seemingly random symbols and operations that give rise to interesting and beautiful patterns. In this post, I'll be presenting a pattern I read about that turned into quite an involved art project. We'll go from fiddling with numbers to live a live and active website by the end. Let's get started!
Playing With Numbers
Take the number 6174. Turn it into two numbers with digits ascending (1476) and descending (7641). Subtract the larger from the smaller to get 7641 - 1467 = 6174. Miraculously, we've come back to the same number in one operation. What if we start with 8028? We'll see that it converges in 2 cycles of this process.
- 8820 - 0288 = 8532
- 8532 - 2358 = 6174
If we start with 1111, it converges to a different value.
- 1111 - 1111 = 0000
While this outcome is interesting, we'll see that any value with all of the same digits will converge to 0000. Let's model all 4 digit numbers with all the same digit in each place as "DDDD". The reverse of "DDDD" is the same exact value, so subtracting from each other will always result in 0000.
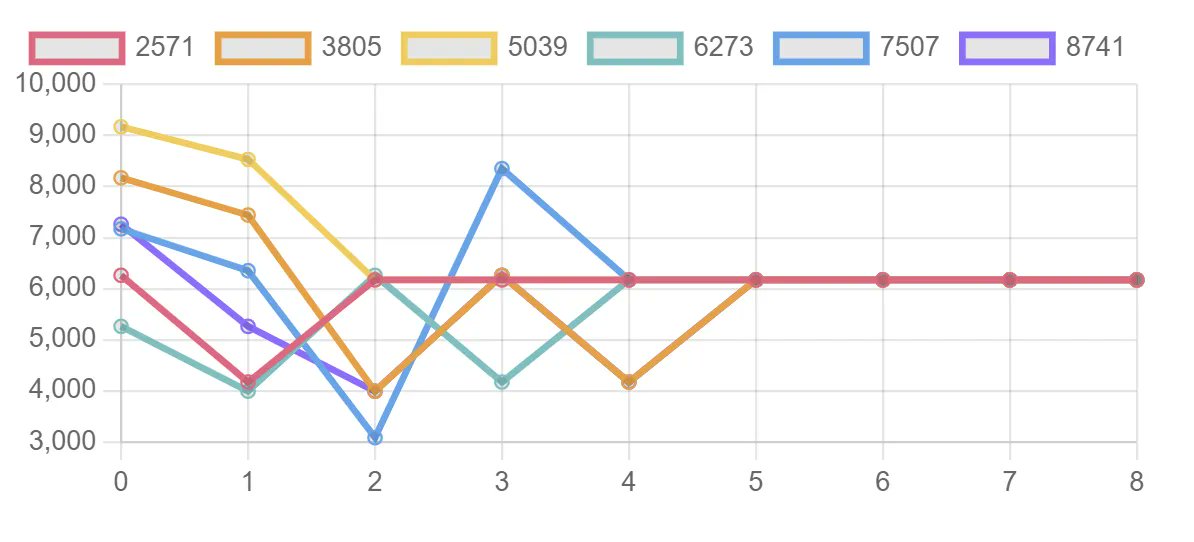
This process and the values for which it converges was discovered by a 20th century mathematician named D. R. Kaprekar. The eponymous routine, "Kaprekar's Routine" was proven to converge to "Kaprekar's Constant", 6174, for all 4 digit values. With different inputs, we can see that they converge with different amounts of iterations. Some 1, some 5 ...etc.
Here's an example for base 10 and length 4:
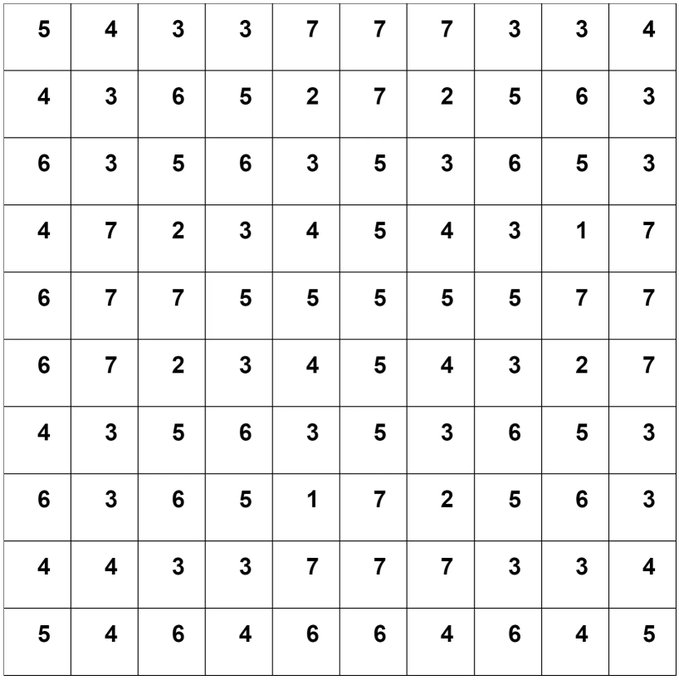
So what if we took this process a step further and took the first 100 valid inputs of length 4 and base 10 and arranged them into a square. This square would have ten rows and ten columns and each cell would be populated with the number of cycles it took the input to converge. Here's what that looks like as an image:
Then using a linear interpolation over the range of the convergence values, we can apply a color scheme to the convergence values in the matrix. The interpolation scheme we're using here is provided by a function in d3 called interpolateReds. We'll get something that looks like this:

Without much massaging, we can generate seemingly random and complex patterns. We can change the way we construct the matrix, change the base, change the length, change the color interpolation ... etc. We can even take the matrices and tessellate them to provide symmetry beyond that provided by the initial input.
Here are a few more examples:
In service of learning more about the visualizations you can make from kaprekar's routine, I've created a website that allows you to make these images within the frontend. Here's the link.


